PID简介

• PID是比例（Proportional）、积分（Integral）、微分（Differential）的缩写
• PID是一种闭环控制算法，它能动态改变施加到被控对象的输出值（Out），使得被控对象某一物理量的实际值（Actual），能够快速、准确、稳定地跟踪到指定的目标值（Target）
• PID是一种基于误差调控的算法，其中规定：误差=目标值-实际值，PID的任务是使误差始终为0
• PID对被控对象模型要求低，无需建模

开环和闭环

要像了解PID，就先要了解什么是开环和闭环

• 开环：控制器单向输出值给被控对象，不获取被控对象的反馈、控制器对被控对象的执行状态不清楚

• 闭环：控制器输出值给被控对象，同时获取被控对象的反馈，控制器知道被控对象的执行状态，可以根据反馈修改输出值以优化控制

PID公式与系统框图

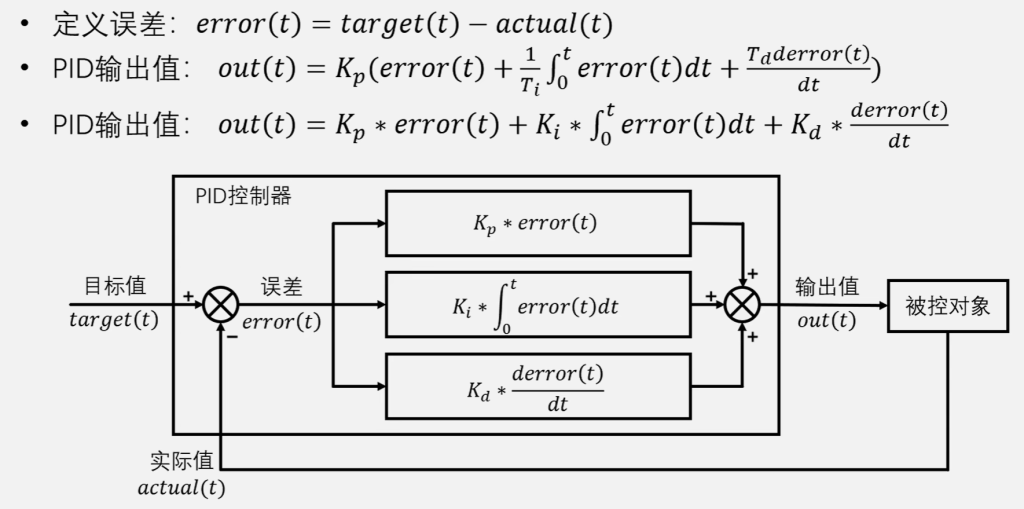
Kp为比例系数

Ti（Ki）为积分时间常数

Td（Kd）为微分时间常数

上面的第二个公式中，如果改变Kp会影响后面两个参数，所以一般采用第三个公式，便于参数调节

即Kp、Ki = Kp/Ti、Kd = Kd*Kp

Kp调节第一项（P）

Ki调节第二项 （I）

Kd调节第三项（D）

比例项（P）

只含有比例项的PID输出值：

• 比例项的输出值仅取决于当前时刻的误差，与历史时刻无关。当前存在误差时，比例输出一个与误差呈正比的值，当前不存在误差时，比例项输出0
• Kp越大，比例项权重越大，系统响应越快，但超调也会随之增加
• 纯比例项控制时，系统一般会存在稳态误差，Kp越大，稳态误差越小

即Kp需要我们自己调一个合适的值，太小，系统响应慢。太大，系统超调严重，甚至自激振荡。

注：自激振荡，即不外加激励信号而自行产生的恒稳和持续的振荡

PID稳态误差

系统进入稳态时，实际值和目标值存在始终一个稳定的差值

稳态误差产生的原因：纯比例项控制时，若误差为0，则比例项结果也为0.被控对象输入0时，一般会自发地向一个方向偏移，产生误差。产生误差后，误差非0，比例项负反馈调控输出，当调控输出力度和自发偏移力度相同时，系统达到稳态

判断是否会产生稳态误差：给被控对象输入0，判断被控对象会不会自发偏移

判断稳态误差的方向：给被控对象输入0，自发偏移方向即为稳态误差方向

积分项（I）

含有比例项和积分项的PID输出值：

• 积分项的输出值取决于0~t所有时刻误差的积分，与历史时刻有关。积分将历史所有时刻的误差累积，乘上积分项系数Ki后作为积分输出值
• 积分项用于弥补纯比例项产生的稳态误差，若系统持续产生误差，则积分项会不断累积误差，直到控制器产生动作，让稳态误差消失
• Ki越大，积分项权重越大，稳态误差消失越快，但系统滞后性也会随之增加

微分项（D）

含有比例项、积分项和微分项的PID输出值：

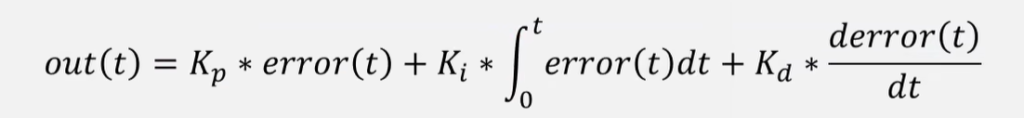
• 微分项的输出值取决于当前时刻误差变化的斜率，与当前时刻附近误差变化的趋势有关。当误差急剧变化时，微分项会负反馈输出相反的作用力，阻碍误差急剧变化
• 斜率一定程度上反映了误差未来的变化趋势，这使得微分项具有”预测未来，提前调控“的特性
• 微分项给系统增加阻尼，可以有效防止系统超调，尤其是惯性比较大的系统Kd越大，微分项权重越大，系统阻尼越大，但系统卡顿现象也会随之增加